DP 풀이방법 5가지 정리 - 백준 11048번 : 이동하기 Python 파이썬

https://www.acmicpc.net/problem/11048

11048번: 이동하기

 

방법1 : Top-Down

문제가 점점 작아지는 방식으로 접근

목적지까지 어떻게 왔는지에 대해서 생각하며 접근

결론에 도달하기까지의 과정에 대해 생각하며 접근

 

 

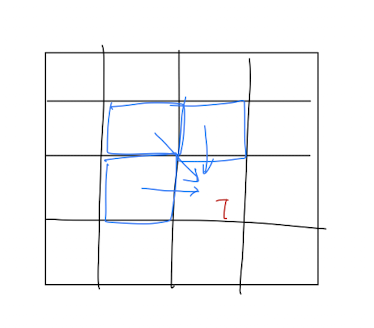
dp[i][j] : (1,1)에서 시작하여 (N,M)까지 가는 중에 (i, j) 까지 갔을 때의 가진 최대 사탕의 수

• 왼쪽에서 온 경우 : (i, j-1)에서 온 경우
• 왼쪽 위에서 온 경우 : (i-1, j-1)에서 온 경우
• 위에서 온 경우 : (i-1, j)에서 온 경우

dp[i][j] 는 (i, j)까지 왔을 때까지의 최대 사탕의 수이므로 각 방향에서 오는 dp와 목적지의 사탕의 개수를 더한 최대값을 다음 dp로 넣는다

 

# Bottom-Up

import sys
input = sys.stdin.readline

N, M = map(int, input().split())

data = []
dp = [[0 for c in range(M)]for r in range(N)]
for i in range(N):
    data.append(list(map(int, input().split())))

tmp_sum1 = 0
for j in range(M):
    tmp_sum1 += data[0][j]
    dp[0][j] = tmp_sum1

tmp_sum2 = 0
for i in range(N):
    tmp_sum2 += data[i][0]
    dp[i][0] = tmp_sum2

for i in range(1, N):
    for j in range(1, M):

        dp[i][j] = max(dp[i-1][j], dp[i][j-1], dp[i-1][j-1]) + data[i][j]


print(dp[N-1][M-1])

 

 

방법2 : Bottom-Up

큰 문제의 정답을 이미 구한 작은 문제의 정답을 이용하여 풀기

기존에 구해져있는 dp값에 지속적으로 새로운 값과 max를 비교하여 쌓아가기

 

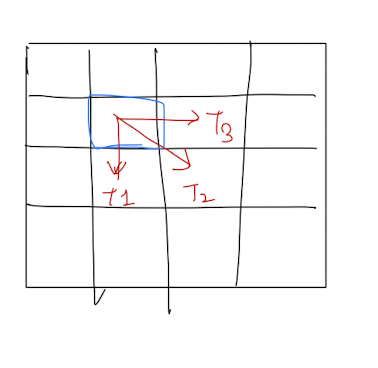
dp[i][j] : (i,j)로 이동할 때, 가질 수 있는 사탕의 최대 수

• dp[i+1][j+1] = max(dp[i+1][j+1], dp[i][j] + data[i+1][j+1]
• dp[i+1][j] = max(dp[i+1][j], dp[i][j] + data[i+1][j])
• dp[i][j+1] = max(dp[i][j+1], dp[i][j] + data[i][j+1])

# Bottom-Up

import sys
input = sys.stdin.readline

N, M = map(int, input().split())

data = []
dp = [[0 for c in range(M)]for r in range(N)]

for i in range(N):
    data.append(list(map(int, input().split())))


dp[0][0] = data[0][0]

for i in range(0, N):
    for j in range(0, M):
        if i+1<N and j+1 <M:
            dp[i+1][j+1] = max(dp[i][j] + data[i+1][j+1], dp[i+1][j+1])
        if i+1<N:
            dp[i+1][j] = max(dp[i][j] +data[i+1][j], dp[i+1][j])
        if j+1<M:
            dp[i][j+1] = max(dp[i][j] + data[i][j+1], dp[i][j+1])

print(dp[N-1][M-1])

 

방법3 최적화 하기

data가 모두 양수라는 조건 때문에 최적화가 가능

칸을 이동 할 수록 사탕의 개수가 증가하는 구조이므로, 최대한 많은 칸을 들리는 것이 유리

따라서 대각선 방향으로 이동하는 것보다 이미 대각선 방향을 거치고 오는 경우(거치고 옆을 돌아서 오는 것)가 더 많은 사탕을 가질 수 있음

위쪽과 왼쪽 방향에서 오는 경우는 모두 (i-1)(j-1)이 고려된 경우가 포함되어 있다.

 

• dp[i][j] = max(dp[i-1][j] , dp[i][j-1]) + data[i][j]

 

# Bottom-Up (최적화)

import sys
input = sys.stdin.readline

N, M = map(int, input().split())

data = []
dp = [[0 for c in range(M)]for r in range(N)]

for i in range(N):
    data.append(list(map(int, input().split())))

dp[0][0] = data[0][0]

for i in range(N):
    for j in range(M):
        dp[i][j] = max(dp[i-1][j], dp[i][j-1]) + data[i][j]

print(dp[N-1][M-1])