[Brute Force] 백준 14500번 - 테트로미노 - Python 파이썬
생각하기
처음에는 테트로미노를 하나씩 N*M 배열위에 배치해서 최대값을 구하는 방식을 생각했지만
아무리봐도 코드가 더러워지고 생각해야할 변수가 많았다
연속하는 인접하는 총4개의 네모
자세히 살펴보다가 아이디어가 하나 떠올랐다
모든 테르미노는 칸이 4개씩이고 변끼리 인접해야 하는 규칙이 있네?
도형기준으로 생각하지 말고 각각의 네모 하나 기준으로 관점을 바꾸어보았다.
이어져있다면 네모가 총 4개가 될때까지 계속 인접한 도형을 먹으면 되지 않을까 하는 생각이 들었다.
줄줄이 소세지처럼 옆의 네모를 타고 그 다음 네모를 타고 그 다음 네모를 타고... 4개까지만 타고 다시 되돌아가면 되는 것이다.
브루트포스 적용시 시간복잡도
브루트포스 문제로 모든 경우를 다 살펴봐도 시간 초과 문제가 안날것은 확인했다.
테트로미노를 회전하고 여러모양을 생성해도 만들수 있는 모양의 최대 개수는 19개이다.
그리고 N*M 배열에는 총 NxM개의 네모가 있고 N,M의 최대는 500이므로
500 x 500 x 19 < 1000000000이므로 충분히 가능하다
예외적인 테트로미노 도형 ㅜ
또 살펴보다가 예외적인 케이스가 하나 있었다
ㅜ 테르미노는 위의 방식대로 하면 구할수가 없네? 정말 ㅗ 같네
이 친구는 recursion을 사용하여 구하면 굉장히 복잡해질 것 같아서 따로 배열을 선언하여 해당 값들을 더해주는 방식을 생각했다.
큐를 사용해서 ㅏ ㅜ ㅓ ㅗ 에 해당하는 도형들을 구현해주었다
나름 많이 생각했다고 생각했지만 결론은 실패...
내가 놓친 것들
방문했던 네모로 가지 말자
사실 해당 문제에 대한 백준 강의를 듣기 전에는 DFS를 활용한 브루트포스 문제라고 생각했는데 DFS가 아니었다.
DFS의 목적은 모든 vertex를 한번씩 방문하는 것
하지만 우리가 짜야하는 알고리즘은
4개가 될때까지 가고 그 과정에서 한번 갔던데는 다시 가면 안된다
예를 들어 1인 네모에서 출발하고 2로 갔는데 다시 1로 돌아가면 왔다갔다하다가 인생 끝날것이다
따라서 visted 함수를 통해서 각 depth에서 방문한 곳은 다시 가지 않도록 해야 한다
다만, 해당 depth를 마친 후에는 visited를 다시 false처리 해야한다
최적화 못하여 시간초과
시간초과가 발생했다!
제일 어려운 결과지만 항상 최적화로 눈을 돌리면 되는 부분이었다.
계산할 필요가 없었는데 계산한 것이 있나? 어차피 최대인데 현재 상태로 최고가 될 수 있나?
현재 아이 상태가 최고가 될 수 있는지 판단하려면 다음과 같은 방법을 쓰면된다
- N*M안에 들어있는 모든 수 중에서 최대값을 구한다
- 재귀를 통해 n개(n<4)개의 네모를 확보했을 때, 나머지 4-n개의 칸이 모두 최대값일 때를 가정
- 그 가정일 때도, 현재의 최대값 max_num을 넘지 못한다면 넌 가망이 없다
이러한 방식으로 쓸데 없는 recursion을 방지할 수 있다.
ㅜ 모양에서는 처리할수 없다 그냥 가자
max_data = max(map(max, data))이렇게 하면 2차원 배열 안의 최대값을 도출할 수 있는 것을 처음 알았다
(map 공부를 좀 해야겠따)...
끄트머리를 고려해주지 못했다
ㅗ ㅜ ㅏ ㅓ 모양의 값을 계산하는 와중에 안쪽만 고려해버렸다
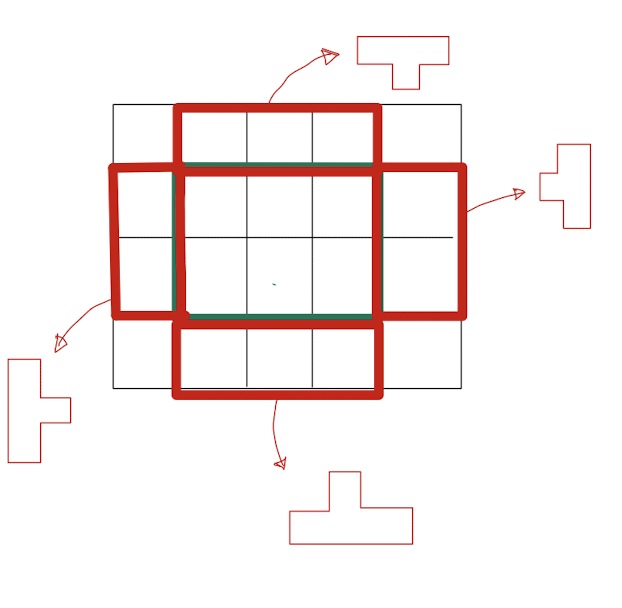
그래서 해당부분이 아닌 곳은 따로 계산해주었다
겨우 한 2일에 걸쳐 푼거 같다.. 많은것을 배울 수 있었던 문제 였다
- 최적화하기
- DFS처럼 보여도 DFS가 아닐 수 있다
import sys
from collections import deque
input = sys.stdin.readline
N, M = map(int, input().split())
data = []
max_num = 0
row = [0, 1, 0, -1]
col = [1, 0, -1, 0]
visited = [[False] * M for _ in range(N)]
for _ in range(N):
data.append(list(map(int, input().split())))
max_data = max(map(max, data))
def check(box, sum, i, j):
global data, N, M, max_num, row, col
if sum + max_data*(4-box) <= max_num:
return
if box == 4:
if max_num < sum:
max_num = sum
return
if i!=0 and j!=0 and i!=N-1 and j!=M-1:
q = deque()
q.append(data[i][j+1])
q.append(data[i+1][j])
q.append(data[i][j-1])
for it in range(3, 7):
tmp_sum = q[0]+q[1]+q[2] + data[i][j]
if max_num < tmp_sum:
max_num = tmp_sum
q.popleft()
q.append(data[i+row[it%4]][j+col[it%4]])
else:
if i==0 and (j!=0 and j!=M-1):
tmp_sum = data[i][j] + data[i+row[0]][j+col[0]] + data[i+row[1]][j+col[1]] + data[i+row[2]][j+col[2]]
max_num = max(tmp_sum, max_num)
if i==N-1 and (j!=0 and j!=M-1):
tmp_sum = data[i][j] + data[i+row[0]][j+col[0]] + data[i+row[3]][j+col[3]] + data[i+row[2]][j+col[2]]
max_num = max(tmp_sum, max_num)
if j==0 and (i!=0 and i!=N-1):
tmp_sum = data[i][j] + data[i+row[0]][j+col[0]] + data[i+row[3]][j+col[3]] + data[i+row[1]][j+col[1]]
max_num = max(tmp_sum, max_num)
if j==M-1 and (i!=0 and i!=N-1):
tmp_sum = data[i][j] + data[i+row[1]][j+col[1]] + data[i+row[3]][j+col[3]] + data[i+row[2]][j+col[2]]
max_num = max(tmp_sum, max_num)
for nIdx in range(0, 4):
nrow = i + row[nIdx]
ncol = j + col[nIdx]
if 0<=nrow<N and 0<=ncol<M and visited[nrow][ncol] == False:
visited[nrow][ncol] = True
check(box+1, sum+data[nrow][ncol], nrow, ncol)
visited[nrow][ncol] = False
for i in range(0, N):
for j in range(0, M):
visited[i][j] = True
check(1, data[i][j], i, j)
visited[i][j] = False
print(max_num)